产品数学课：如何理解个性化推荐里的数学原理？

6月份是高考以及毕业的月份，这种时候特别适合老人家怀旧。离开课堂三年，课本上学的知识几乎都还给了老师。写这篇文章即是加深自己对个性化推荐的理解，也想趁着高考时回顾下高（中）数（学）。

一、什么是个性化推荐？

个性化推荐，是系统的智能推荐。为什么豆瓣的私人FM特别符合我们的音乐品味，又为什么电商应用总是知道我们想买什么？

个性化推荐的原理使用较多的是这3种方式： 基于内容的推荐、基于用户的协同过滤、基于物品的协同过滤

这3种推荐方式的核心则是 计算相似度 。

二、这三种推荐方式是什么？

介绍相似度的计算之前，先为大家简单介绍一下这三种推荐方式。

2.1 基于内容的推荐(Content-Based Recommendation)

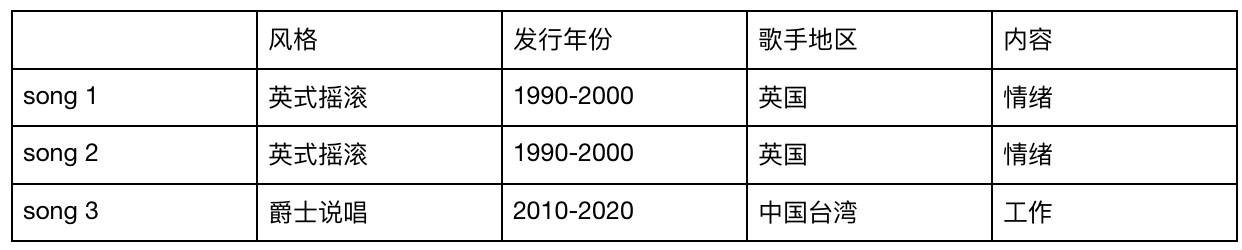
表1-内容相似度举例

在上表表1的对比中，song 1与song 2，在风格、发行年份、歌手地区及内容上是相近的或者是相同的，这两首歌的相似度更高。

song 3仅有发行年份与前面两首歌匹配，其他则完全不匹配，song 3与前两者是完全不相似的。

基于内容的推荐，本质是 “你喜欢某一事物，给你推荐近似的事物。”

你喜欢song 1，系统为你推荐song2。

2.2 基于用户的协同过滤（User-based CF）

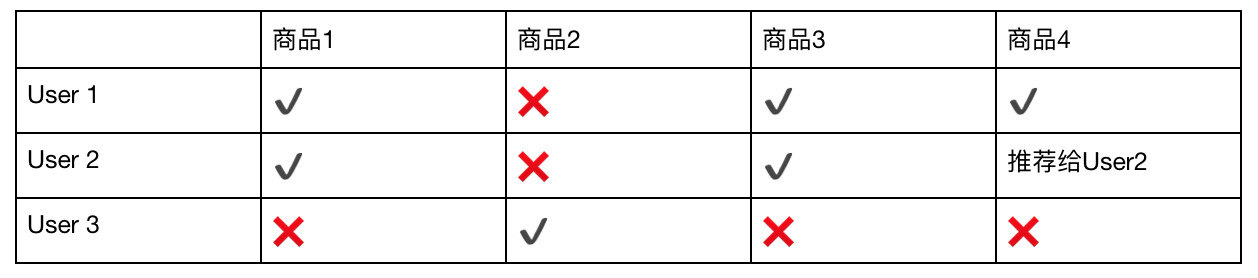
表2-用户相似度举例

基于用户的协同过滤，通俗的解释是： 和你相似的用户还买了什么？

我们会先 找到相似的用户 ，然后 找到此类用户喜欢的且目标用户未接触的物品 ，将其推荐给目标用户。

上表表2中，我们先找到相似的User 1和User 2（下文简称U1、U2） , 他们都购买了商品A、C且未购买商品B。

然后将U1买过的且U2没买过的商品D ， 推荐给U2。

U3则仅购买商品B，其他的都未购买，推荐系统会认为他与U1、U2没有什么关联，所以我们不会对U3推荐U1和U2购买的商品。

2.3 基于物品的协同过滤（Item-Based CF）

基于物品的协同过滤， 以物品为核心，它是对基于用户的协同过滤的一种改良 。

理解为： “买了这款商品的用户，还买过什么。”

图2-京东图书首页

前阵子我购买了《推荐系统实践》一书，在上图中，京东给我推荐了产品相关书籍《幕后产品》以及数据相关书籍《商业智能数据分析》。

当然万一我是半个研发呢，所以给我又推荐了一本《深入浅出Prometheus》。

2.4 三种推荐方式的区别

理解完这三种推荐方式，我们来看看他们之间的区别。

1）基于物品的协同过滤与基于内容的推荐

内容和物品都是事物的一种，2者似乎都是在计算物品的相似性？看起来是相同的。

但实际上基于内容的推荐，更倾向于 两件事物是接近的、相似的 ， 与用户的行为无关 。而基于物品的协同过滤则 与事物是否相似关系较小，更多与用户行为有关，是有顺承关系的。

2）基于物品的协同过滤与基于用户的协同过滤

基于 用户 的协同过滤， 是先找相似的人，再找相似的人喜欢的物品。

基于 物品 的协同过滤， 则是找到和某个物品相关的物品。

当物品数量、特征相对固定的情况下，更多采用基于物品的协同过滤 。 因为 相对稳定一定程度上意味着不需要实时计算 ，通过离线的运算，对服务器的压力就很小了。

当物品和用户量都非常大，这样会造成购买的物品重叠性较低，我们很难才能找到相似的用户，Item-Based CF就不适用了。

而在如内容类媒体，微博、新闻网站等，物品（内容）的数量、特征都在不断的变化，去计算物品的相似度性能消耗反而更大了。而新闻媒体更倾向于群体的喜好，这个时候使用User- Based CF也更加的合适。

初步了解完这三种推荐方式，我们便回到它们的核心 ：相似度的计算。

三、相似度怎么计算

相似度常见的计算方式是 余弦相似度、欧几里德距离、Jaccard相关系数。

下文则是对 余弦相似度 及 欧几里德距离 的理解。

数学课正式开始（敲黑板）。

图3-多举栗子挂柯南

3.1 余弦相似度

图4-余弦相似度公式

最开始我看到这个公式时，有种 《个性化推荐：看到公式就放弃》 的感觉。可是作为一枚产品汪，我觉得，我还是要抢救一下。

于是我试着将公式拆解，

similarity： 相似性；类似性。

cos(θ)： 在直角三角形中=领边/斜边； 在空间中=空间中两个向量夹角的余弦值。

图5-直角三角形回忆

连起来说， 相似度=空间中两个向量夹角的余弦值。

在线性代数上：“ 向量是多维空间中从原点出发，具有大小及方向的有向线段。”

当 向量的夹角越小，方向则越接近 。代表着 内容、用户、物品的向量方向越接近 ，则他们越相似。

而根据图3的公式计算，夹角越小，cos(θ)越趋近于1。所以前辈们将余弦值当成量化相似度的手段，当余弦值趋近于1，二者则是相似的，趋近-1的看做是不相似的。

可是， 向量为什么能够代表内容，代表用户呢？

图6-向量的夹角

向量代表着在N维空间中的方向， 它的坐标表示法是： α=（x，y）， 这个表示法是指向量α在x轴方向以及y轴方向的坐标。不准确但通俗的理解为： 在x轴方向的趋同度以及y轴方向的趋同度。

图7-向量类比举例

换个说法，不是向量，x轴和y轴。而是等于歌曲，发行年份和风格近似度。

song2=（95%，1997），即song2这首歌发行年份在1997年，歌曲风格与Brit-Pop的匹配度有95%。

图8-三维向量举例

理解了2维的向量，我想理解3维、多维会更加容易。

那么回到刚刚的问题：“向量为什么能够代表内容，代表用户呢？”

从刚刚的例子我们可以推导出， 内容或者用户本质上是在不同维度拥有相关性的坐标

组成内容、用户的维度绝对不止于3维， 当维度越多，我们就会被量化的越彻底，相似度会被计算的越准确。

在上文介绍余弦相似度的时候，一直在强调一个词： 方向 。余弦相似度注重维度之间的差异，不注重数值上的差异。这其实也是余弦相似度不足的地方。

表3-余弦相似度的不足

表3中，User 1，给Blur乐队和Oasis乐队分别评了1颗、2颗星，而User 2则是评了4颗、5颗星。

图9-表3向量表示

将其在二维空间中表示，我们会发现，代表User 1和User 2的夹角非常的小，用余弦相似度来计算则会发现余弦值等于0.97，这两名用户会是非常相似的，这真的太糟糕了。

而 对于强调数值差异的事件相似度，我们要用什么方法来计算呢？

一种方法是， 利用维度间均值是调整余弦的相似度， User 1，User 2对两支乐队评分的平均值是3。

我们将2名用户的评分减去3，则会变成User 1(-2,-1)，User 2(1,2)，再次通过余弦相似度计算，得出-0.8，这个时候的差异值就非常大了。

另一种方法，则是利用欧几里德距离。

3.2 欧几里德距离

图10-欧几里德距离

欧几里德距离，它也叫欧式距离。上文我们提到的向量，也称欧几里德向量。

这个公式实际上是 二维空间中两点的距离，多维空间中向量的距离。距离越小，则差异越小，越接近。

由于我们习惯相似度与1进行类比，越接近于1相似度越高。所以前辈们对欧式距离进行了归一化处理，通过将函数值加1，并取其倒数的方法来构造欧几里得相似度函数。

其中加1的目的则是为了避免分母为0。

图11-欧几里德相似度函数

将上文表3的值代入欧几里德相似度函数，SimDistance≈0.2，那我们也能够得出正确的结论，User 1以及User 2并不相似。

欧氏距离体现事件数值的差异 ，如：GMV的增长金额，用户的消费频次等。类似GMV这类数字，很可能增速趋近，但是增长的金额却大不相同。

欧氏距离和余弦相似度分别适用于不同的数据分析模型，欧氏距离适用于数值差异敏感的推荐，而余弦相似度用于方向上的差异，更多用于兴趣的相似度及差异。

最后

以上，是对个性化推荐一部分笔记，在个性化推荐落实到应用层面，其实还有 冷启动、过滤、加权以及融合 等等。这方面有更专业的大佬已经做了许多的总结，就不多献丑了。

希望这篇笔记能让大家有所收获。如有不正之处，欢迎大家指出以及交流。

本文由 @WISE原创发布于人人都是产品经理 ，未经许可，禁止转载。

题图来自Unsplash，基于CC0协议

作者暂无likerid, 赞赏暂由本网站代持，当作者有likerid后会全部转账给作者（我们会尽力而为）。


Support author:
Author's Filecoin address:
Or you can use Likecoin to support author: