對稱簡潔除了美也很實用：幾個應用對稱思維來破解的數理益智問題

Sharer: 泛科學 August 15, 2019 at 4:00 am

Link Share :https://pansci.asia/archives/166115 - via RSS

對於物理學家來說，美麗意味著對稱和簡單。如果理論是美觀的，這意味著它具有強大的對稱性，可以以最緊湊、最經濟的方式解釋大量數據。更確切地說，如果我們在方程式之內互換變數時，方程式能保持不變，那麼方程式將被認為是美觀的。

──Michio Kaku 理論物理學家、科普作者

語云愛美是人類的天性，儘管情人眼裡出西施，每個人的審美觀點可能不同，但基本上「美」是脫不了對稱與簡潔！你聽說過鼻樑不正、左眼大右眼小的美女或俊男嗎？事實上讓人望而生畏的獅子或老虎，其長相也都具有左右對稱的美！花之所以美，更是脫離不了其對稱性。

物理學家也是人，因此當然也愛美，例如在〈近代物理的先驅：馬克斯威〉一文裡，筆者就談及馬克斯威看到了實驗導出之 電磁方程式 缺少對稱之美，因此人為加入「位移電流」，使他在 1865 年能導出電磁波的存在，並證明光是一種電磁波。現在，對稱已經是物理學家的一個主要工具：在尚不清楚基本粒子的作用時，他們就是靠對稱引導而發展出「標準模型」！

對喜好數學和物理的科普讀者，「對稱」與「簡潔」的概念也能幫助我們解決一些學習過程、或日常生活中所碰到的問題。

動動腦，思考一下這些數理問題吧！

[a] 人人都知道運動是「相對的」，因此說「太陽是以橢圓的軌跡繞地球運動」，事實上應該也是不錯的；可是為什麼科學家一定要說「地球繞太陽」呢？
[b] 四隻螞蟻分別佔據了正方形的 A、B、C、D 四個角落，每隻螞蟻均以等速永遠朝著另一隻螞蟻前進（不需沿著正方型的邊，如A→B、B→C、C→D、D→A），最後牠們會碰在一起嗎？
[c] \( \iint_{a}^{b} \frac{x+y}{\sqrt{x}-\sqrt{y}}dxdy=? \)
[d] 一條固定長度的繩子彎曲折成四角形，最大面積的四角形之兩邊比為何？
[e] 用一條固定長度的繩子彎曲折成任何形狀，最大面積的圖形為何？
[f] 因為重男輕女的關係，世界組織規定：只要一生男孩就不能再生了；但如果是女孩，則一定要繼續再生，一直到生男孩為止。如果生男生女的機率完全一樣，那麼長時間以後，女性人口是不是會比男性多？
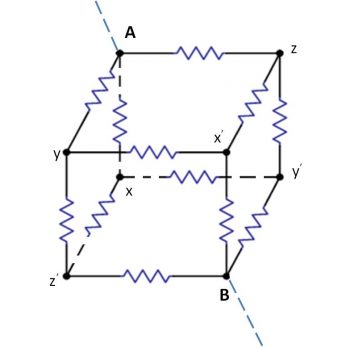
[g] 如下圖，所有的電阻都是 Ω，那麼 AB 兩點間的等效電阻是多少？
[h] 一個平面的正七角形，每個角上均帶 +Q 電荷，中心點的電場方向為何？

都想出來了嗎？看看解答怎麼說

[a] 答案是：運動的確都是相對的，如果將行星的運動解釋為地球及其他 8 個行星圍繞太陽，則它們的軌跡方程式將都是非常簡單（橢圓）——可以用最緊湊、最經濟的方式解釋大量數據。反之，如果認為地球是太陽系的中心，則除了太陽軌跡是橢圓外，其它行星的軌跡都將非常複雜！

如果認為地球是運行的中心，那就要用很複雜的系統才能解決某些觀察到的現象如「水星逆行」，上圖即為地心說的其中一個版本。圖／wikimedia commons

在相信上蒼不會那麼笨手笨腳，簡單就是美的「盲目信仰」下，「地球繞日」說自然佔了上風！你說科學家不是愛美愛得一塌糊塗？！

[b] 因為這四隻螞蟻永遠等速朝著另一隻螞蟻運動，螞蟻的相對位置會形成越來越小的正方形，所以最後會在中心碰在一起。
筆者對這一問題特別有印象，在籌劃創辦「科學月刊」（1969 年）之時候，由一位學數學的同學提出來的；當學物理的還在思考著如何找出其運動方程式時，筆者已衝口而出謂「當然碰在一起」！筆者當時閃過腦中的想法是：如果牠們最後是在那裡繞圈子永遠不相逢，那麼圈子應該是多大的？從對稱的觀點來看，任何圈子不是都應該可能嗎？只有中間的一點是特別的「圈子」，因此毫無疑問地，牠們將在哪裡碰在一起！
到了寫這篇文章，筆者發現當時的想法事實上是錯誤的：因為永遠朝著另一隻螞蟻運動，是不可能形成圈子的（見圖），只能形成越來越小的正方形，所以最後一定要碰在一起！單隻螞蟻的路徑會是逐漸內縮的螺旋型，但略微想了一下，覺得運動方程式事實上很難找註1！

永遠朝著另一隻螞蟻運動，是不可能形成圈子的。圖／作者提供

[c] 此一積分具有（x,y）互換的「反」對稱，因此答案為零。
一個大家所熟悉的例子是：如果一個函數\( f(x) \)具有 y-軸的「反」對稱{\( f(-x)= -f(x)\)}，則從 -a 到 +a 的積分應等於零。這一題目的對稱軸是同時與 x-軸及 y-軸成 45 度的斜線。
不用對稱之運算證明如下（第 1 個等號「=」是 x、y 互換的結果；第 2 個等號「≅」號是因 x、y 只是用來表示變數，與用什麼符號來表示無關：例如 ax2+bx+c=0 與 ay2+by+c=0 根本是相同的方程式，只是用不同的符號來表示變數而已）：

\( \iint{a}^{b} \frac{x+y}{\sqrt{x}-\sqrt{y}}dxdy\) \(=-\iint{a}^{b}\frac{y+x}{\sqrt{y}-\sqrt{x}}dy dx \) \( \cong -\iint_{a}^{b}\frac{x+y}{\sqrt{x}-\sqrt{y}}dx dy\)

將最後一項移到左邊與第一項合併

\( 2\iint_{a}^{b}\frac{x+y}{\sqrt{x}-\sqrt{y}} dx dy=0 \)

[d] 答案是邊長一樣的 正方形 。
因為如果邊長不一樣，那麼我們不免要問，為什麼是這一個長方形、而不是另一個長方形呢？只有正方形是一個特殊的長方形！
[e] 基於上面的邏輯，相信許多讀者已經知道答案了：當然是圓形！
這裡的邏輯事實上是與前面有點不一樣的，因為任何正多角形事實上是都很「獨特」的，但同樣的問題還是存在：如果是正六角形，為什麼不是正五角形和正八角形呢？圓形具最高的對稱性，沒有這一問題！
在這裡筆者想到了一個自然界的現象：為什麼許多皮膚病多是呈圓形的呢？固定長度，圓形面積最大；反之，固定面積，圓形邊長應該最短：這不是最有利於細菌反抗「外面」的攻擊嗎？城堡很少是圓形的，就這點來看，人類顯然還是比細菌笨了一點！同樣的道理，體積一樣、面積最小的立體結構應是圓球——這是否與自然界中許多動植物（如細胞或水果）都是以圓球形狀出現有關？
[f] 新婚生小孩，除了一半家庭是只有一個男孩的外，其他一半家庭最後都是女多於男（或相等）；因此直覺的反應可能是：千百年後，女的將比男的多！可是換一個角度看，每天新生出來的小孩總是男、女數相等，怎麼可能破壞男女的平衡呢？雖然決定誰可以繼續生小孩時，男女的平等被破壞了，但這一條件，並沒有破壞決定生男育女機率相等的「物理定律」，因此應該不會影響男女數的平衡。事實上，問題之條件（只要一生男孩就不能再生了；但如果是女孩，則一定要繼續再生，一直到生男孩為止）完全是故意用來擾亂你的思路的：任何一刻之男女數的增加都是相等的，與什麼樣的夫妻可以再生無關。
在「時間的方向性」一文裡，筆者提到了大物理學家波茲曼（Ludwig Boltzmann）於 1872 年用牛頓力學導出具有時間方向性的「H-理論」；可是牛頓力學具有時間對稱性，怎能產生一個不具時間對稱性的結果呢？因此「H-理論」提出後便立即受到攻擊。我們不能在這裡犯同樣的錯誤。
[g] 用傳統的線路分析將是非常困難的（超過普通物理程度）註2；但利用對稱則輕而易舉。以通過 AB 兩點的連線為軸，這網絡具有一個旋轉 120 度的正三角形對稱；因此（x、y、z）三點可視為同一點 A' ──永遠具有同樣的電位。同樣地，（x'、y'、z'）三點也可視為同一點 B'。AA' 間共有三個相同的電阻並聯，故其等效電阻為 Ω/3。同樣地，BB' 間也共有三個相同的電阻並聯，故其等效電阻亦為 Ω/3。A'B' 間則共有六個相同的電阻並聯，故其等效電阻為 Ω/6。這三個等效電阻串聯，故 AB 間的等效電阻為 5Ω/6！

用傳統的線路分析非常困難，但利用對稱則輕而易舉。

[h] 因為對稱的關係，任何方向均應該有七個對稱方向。如果答案只能有一個方向，不用三角幾何計算，我們就應該知道答案只能為「零電場」。

結論

以上是筆者想到或者在網路上看到的、可以用「對稱」解決的幾個問題——相信應該還有很多類似的問題。從[c] 題我們可以看出：如果知道怎麼直接計算，我們根本不需要「對稱」！但如果命題具有對稱性，則像[a] 及[g] 一樣，我們根本可以完全不知道怎麼計算，就可以輕輕鬆鬆地得到答案：這正是數學上「對稱理論」—「群論」—的巨大力量！

註解

真正的意思是：筆者還不知道怎麼找運動方程式來解決這一個問題。不怕被方程式嚇倒的讀者可以參考 4 Bugs chasing each other differential equation（裡面有幾種解決的方法）。
所謂「普物程度」就是筆者所知道之「透過電阻串聯及並聯的理論來簡化」（事實上大概不可能用此一理論來解決這一個問題）。想知道電機系的學生如何解決此一問題的讀者可以參考 The resistor cube problem。

動動腦，思考一下這些數理問題吧！

都想出來了嗎？看看解答怎麼說

結論

註解

延伸閱讀