白白说算法：相亲中的马尔科夫模型

按照未来互联网的发展趋势以及日趋激烈的人才竞争中，产品经理也须掌握基础的技术算法。因此，本文以相亲为例，介绍了什么是马尔科夫模型。

大家好，我是白白，第一时刻来讲讲算法系列。

产品经理是否需要懂技术，对于这个问题互联网圈看法各不相同。

白白看来，随着未来互联网的发展，按照正常的产品经理职业发展路径，还是需要了解一些技术的内容。产品经理需要了解技术的基本框架，但不一定需要了解所有技术细节。人工智能领域，产品经理需要了解算法的基本原理，以及如何将实际问题转化为算法问题。

白白作为一名AI产品经理，准备持续写一写算法的内容，争取用最简单的语言告诉大家每种算法的逻辑。

一、马尔科夫模型

有一天白白去相亲，见了2个人，上午一个下午一个。

两个小姐姐都不错，这下白白突然不知道应该选哪个（其实两个妹子都没看上我），后来有个算法的同事过来支招，毕竟是结婚过日子么，那还是要考虑充分。

有一种算法的含义是每种状态，只与之前的一个或多个状态有关，也就是说我们可以根据小姐姐之前的状态再综合评价。

白白思考了10秒，觉得好像挺有道理，毕竟现在看着还不错，万一隐藏了什么呢？

所以还是要看看小姐姐的上一个状态。从人生的角度来讲，女孩的上一个状态，也就是她妈妈了。这种每个状态由之前的1个或多个状态决定的模型，我们称为马尔科夫模型。

马尔科夫模型中很多关系使用概率描述的，比如女孩的妈妈很白，那么女儿也很白的概率是90%，女孩妈妈是性格好，女儿也性格好的概率为70%。下图展示了母亲和女儿性格之间的概率关系。

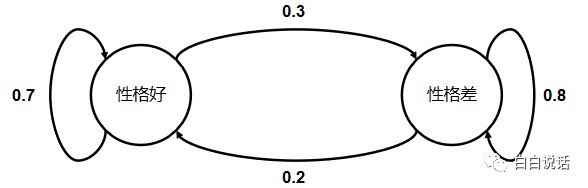
由上图可列出表格：

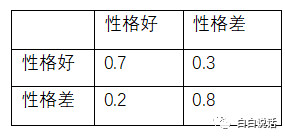
马尔科夫模型有三个要素：

1. 状态：性格好、性格差
2. 初始向量：在系统定义时间为0时，状态出现的概率。比如从女儿妈妈出现的时间算起认为是系统的0时，那么她妈妈性格好或性格差的的概率就是初始向量。
3. 状态转移矩阵：上图列出的表格就是状态转移概率，用于描述状态之间的转换。

在实际问题中，有关序列的问题很多都可以用马尔科夫模型来求解，例如股票的量化分析、新闻摘要提取、用户行为预测等。

二、隐马尔可夫链

我们即使知道马尔科夫模型的3个要素，还是无法做出良好判定。因为我们观察到的状态中，很可能还包含有隐藏状态。比如我们看到小姐姐和她妈妈确实都不错，但是或许隐藏着小姐姐没准已经有男朋友了，她现在是在找备胎。

来换个阳光的例子，假如小姐姐打了你一巴掌，打人只是表象，真实的隐藏状态是她的心情。打人不一定表示她不开心，打人这个现象对于她是否开心，也有相应的概率。所以对于模型而言，必须要考虑多种情况才能对状态有完整的描述。

针对以上的情况，还有一种与马尔科夫模型很像的模型，称为隐马尔科夫链。

在隐马尔可夫模型中有两条链，一条称为可见状态链，一条称为隐藏状态链。每个状态之间依然是一种序列的关系。

如下图中，X表示女孩的实际的某个状态，但是我们看不到，这就是隐藏状态链。O表示女孩的性格情况，我们只能观察的O这个状态，这就是可见状态链。

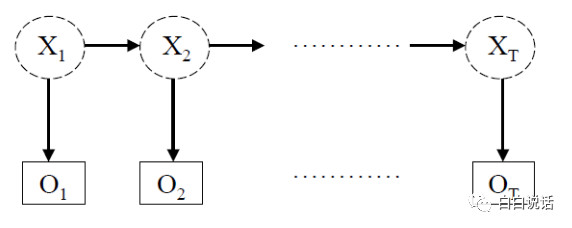
1. 隐马尔可夫模型主要解决的问题

隐马尔可夫主要围绕以下三类问题：

1. 给定一个模型，求某个观察序列O的概率
2. 给定模型和观察序列O，求可能性最大的X序列
3. 对于给定的观察序列O，调整隐马尔可夫模型的参数，使得观测序列O出现的概率最大

其中第二类问题是我们最常见的，在语音识别、文本分析等领域有着广泛应用。简单来讲，就是通过我们看到的可见状态链来求解隐藏状态链的相关活动。

当和姑娘相处了一段时间之后，会摸清楚她大概的品性，这就是初始概率。比如大部分时间是开心的，或者开心与不开心各占一半。

隐马尔科夫链模型有四个要素：状态、初始向量、状态转移矩阵、输出矩阵。

前三个与马尔科夫模型几乎没有区别，输出矩阵指的是由隐藏状态到可见状态的输出概率。

例如小姐姐心情不好，可能打人的概率，可能购物的概率等，这些都是输出概率。我们可以建立隐马尔可夫模型，通过小姐姐的表现计算她是否开心。

建立隐马尔可夫模型：心情有2个状态（不开心、开心），但是我们无法直接观察到心情（心情状态对我们是隐藏的），我们只能观察到小姐姐的行为（撒娇、购物、打人），我们认为小姐姐的心情与上一时刻的心情有关，即这个系统构成隐马尔可夫链。

我们已知妹子的长期的一个心情分布概率（初始情况）：P={开心：0.6，不开心：0.4}

转换概率分布为：

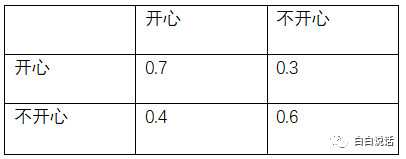
在相应的心情下，妹子进行的活动的输出概率分布为：

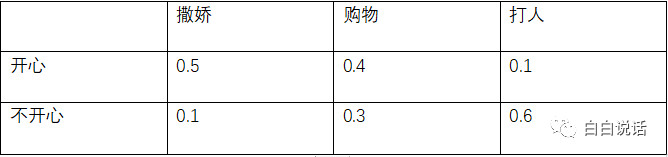
计算第一时刻的心情情况：

• P(第一时刻开心)=P(撒娇|开心)P(开心|初始情况)=0.50.6=0.30
• P(第一时刻不开心)=P(撒娇|不开心)P(不开心|初始情况)=0.10.4=0.04

第一时刻开心的概率比较大，于是我们可以认为第一时刻是开心。

假设知道妹子第二时刻在妹子在购物，计算第二时刻的心情情况：

• P(第一时刻不开心，第二时刻不开心)=P(不开心|第一时刻)P(不开心->不开心)P(购物|不开心)=0.040.60.3=0.0072
• P(第一时刻不开心，第二时刻开心)=P(不开心|第一时刻)P(不开心->开心)P(购物|开心)=0.040.40.4=0.0064
• P(第一时刻开心，第二时刻开心)=P(开心|第一时刻)P(开心->开心)P(购物|开心)=0.300.70.4=0.084
• P(第一时刻开心，第二时刻不开心)=P(开心|第一时刻)P(开心->不开心)P(购物|不开心)=0.300.30.3=0.027

可以看到第二时刻最可能的是开心。

假设知道第三时刻妹子把你给打了，我们来算算各种情况的概率：

• P(第二时刻不开心,第三时刻不开心)=P(不开心|第二时刻)P(不开心->不开心)P(打人|不开心) =0.0270.60.6=0.00972
• P(第二时刻不开心,第三时刻开心)=P(不开心|第二时刻)P(不开心->开心)P(打人|开心) =0.0270.40.1=0.00108
• P(第二时刻开心,第三时刻开心)=P(开心|第二时刻)P(开心->开心)P(打人|开心) =0.0840.70.1=0.00588
• P(第二时刻开心,第三时刻不开心)=P(开心|第二时刻)P(开心->不开心)P(打人|不开心) =0.0840.30.6=0.01512

我们可以认为，第三时刻的心情是不开心。

通过上面三个时刻的计算，我们可以得出隐藏状态的序列：开心->开心->不开心。

这就是隐马尔可夫链模型的简单介绍。

#专栏作家#

白白，人人都是产品经理专栏作家。医药行业资深产品专家，负责人工智能行业类产品综合架构与技术开发。在行业云产品架构，药物设计AI辅助、医疗知识图谱等领域有深入研究。

本文原创发布于人人都是产品经理。未经许可，禁止转载。

题图来自Unsplash，基于 CC0 协议

作者暂无likerid, 赞赏暂由本网站代持，当作者有likerid后会全部转账给作者（我们会尽力而为）。


Support author:
Author's Filecoin address:
Or you can use Likecoin to support author: